Techmax 36: Mit Quanten rechnen

Auf dem Weg zum Quantencomputer und Quanteninternet

© MPI für Quantenoptik

Quantencomputer und Quanteninternet – das klingt magisch. Tatsächlich könnten künftige Quantencomputer spezielle Aufgaben lösen, an denen selbst heutige Supercomputer scheitern. Und Quantennetzwerke könnten Quantencomputer zu leistungsfähigen Quantenclouds verbinden. Bis dahin ist allerdings noch viel Grundlagenforschung nötig, wie sie Mari Carmen Bañuls und Gerhard Rempe betreiben. Sie leitet eine Theorie-Arbeitsgruppe am Max-Planck-Institut für Quantenoptik in Garching, er ist dort Direktor.

Stellen wir uns eine Alice vor, die ein Auslandsschuljahr in Kanada verbringt. Ihre Mutter, eine Physikerin, hat ihr und ihrem daheim gebliebenen Bruder Bob je einen Würfel mit Spielanleitung gegeben. Vor Alices Abreise mussten beide ihre Würfel kurz aneinander klicken. Nach Alices Ankunft in Toronto sollen beide einhundert Mal würfeln, die Würfe notieren und dann ihre Listen vergleichen. Seltsam, denkt Alice, dabei können doch nur Zufallszahlen herauskommen, die nichts mit Bobs Würfelei zu tun haben. Im Videochat zeigt aber der Vergleich, dass es eine seltsame Verbindung zwischen den Würfeln gibt – über mehr als 6000 km Entfernung hinweg! Würfelte Alice eine 1, erhielt Bob eine 6, bei Alices 2 erzielte Bob eine 5 usw.: Die beiden Würfel fielen immer auf die entgegengesetzten Seiten. Auf Alices Smartphone erscheint nun neben Bobs Kopf der ihrer Mutter. „Das ist ja Zauberei, Mama“, beschwert sich Alice: „Dabei hast du doch immer behauptet, es gäbe keine Zauberei, nur Tricks!“ „Es handelt sich um Quantenzauberei“, erklärt die Mutter lachend: „Es sind Quantenwürfel, die ihr durch Aneinanderklicken vor deiner Abreise miteinander verschränkt habt.“

Sensible Verschränkung

Jetzt kommt der Spoiler: Quantenzauberwürfel, die man einfach so anfassen kann, gibt es nicht. Aber die Verschränkung existiert, allerdings eher in der Mikrowelt kleinster Teilchen, wo die Quantenphysik regiert. Durch sie können zwei räumlich getrennte Quantensysteme wie diese Würfel ein gemeinsames Quantenobjekt bilden. Macht man dann eine Messung an einem der beiden Systeme, hier wäre es ein Würfelwurf, dann legt man automatisch auch den Zustand des anderen Quantensystems fest. Vor der Messung sind beide Zustände unbekannt und nicht festgelegt! Letzteres ist eine wichtige Eigenschaft der Quantenwelt. Da verschränkte Objekte räumlich weit voneinander getrennt sein können, spricht die Physik von „Nichtlokalität“. „Lokalität“ entspräche Alices Erwartung, dass ihre und Bobs Würfel komplett unabhängig sein sollten. Sie ist eine Eigenschaft der klassischen Physik, die in unserer Makrowelt der „anfassbaren“ Dinge gilt.

Albert Einstein erkannte als einer der Ersten, dass die noch neue Quantenmechanik diese „geisterhafte Fernwirkung“ erlaubte, wie er das spöttisch nannte. Für ihn war das ein Beleg für die Unvollständigkeit der Quantenmechanik. Doch ab den 1960er-Jahren und vor allem den späten 1970er-Jahren gelangen zunehmend Experimente, die bewiesen, dass die Verschränkung existiert. Vor allem der Fortschritt der Lasertechnik (s. Techmax 6) erlaubte ausgefeilte Experimente, in denen immer weiter voneinander entfernte Lichtquanten, Photonen, verschränkt blieben. Die Quantenmechanik beschreibt die Natur in der Mikrowelt also vollständig. Aber warum gibt es Alices und Bobs Quantenwürfel ebenso wenig wie den Unsinn von „Quantenheilungen“? Der Grund: Die Verschränkung von Quantenteilchen ist extrem empfindlich. Jede kleinste Störung entspricht in der Quantenwelt einer Messung. Sie legt den Quantenzustand der verschränkten Teilchen fest und zerstört die Verschränkung. Allein schon die Wärmebewegung der Atome in unserer Umwelt reicht aus. Deshalb können handwarme Würfel aus vielen Milliarden Atomen wie die von Alice und Bob niemals verschränkt sein. In der Physik heißt diese zerstörende Wirkung „Dekohärenz“. Kohärenz kann man sich grob wie Bobs Hobby, einen Ruderachter, vorstellen: Wenn sich Bobs Team so eingetaktet hat, dass es wie ein einziger megastarker Ruderer arbeitet, befindet es sich in einem kohärenten Zustand. Bringt aber ein im Fluss vorbeifahrendes Frachtschiff das Boot so ins Schwanken, dass die Ruderer außer Takt geraten, dann schlägt die Dekohärenz zu. Wegen dieser Empfindlichkeit ist das Forschungsgebiet der Quanteninformation sehr anspruchsvoll, denn die Verschränkung ist das Hauptwerkzeug. Ziele sind der Bau von Quantencomputern und Quantennetzwerken bis hin zum globalen Quanteninternet. Gerhard Rempe ist ein Pionier der Forschung an Quantennetzwerken. Für ihn geht deren Entwicklung mit der des Quantencomputers „Hand in Hand“.

Ein Netzwerk aus Qubits

Zuerst müssen wir aber den Grundbaustein der Quanteninformation kennenlernen: das Quantenbit. In unserer Digitaltechnik gibt es das Bit als kleinste Informationseinheit. Es kann nur die zwei Werte 0 oder 1 annehmen, also „Strom aus“ und „Strom an“. Das Quantenbit (Qubit) ist das Gegenstück zum Bit. Es kann ebenfalls 0 oder 1 annehmen – darüber hinaus aber noch unendlich viele Werte dazwischen (Abb. A). „Die Zustände 0 und 1 sind dann überlagert“, erklärt Rempe: „Das nennt man Superposition.“ Erst wenn man eine geeignete Messung an dem Qubit macht, springt es entweder in 0 oder 1. In dieser Überlagerung steckt theoretisch die Rechenmacht von Quantencomputern für spezielle Aufgaben. Für Qubits eignen sich im Prinzip alle Quantensysteme, die zwei verschiedene Zustände und deren Überlagerung erlauben. Das können zum Beispiel einzelne Atome sein, die in einer Falle aus starkem Laserlicht gefangen sind. Damit arbeiten Gerhard Rempes Forschungsteams.

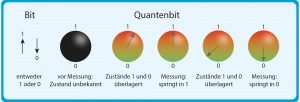
Abb. A: Bits und Quantenbits. Ein „klassisches“ Bit für einen herkömmlichen Computer kennt nur die Zustände 0 und 1. Das Quantenbit kann auch beliebige Überlagerungen beider Zustände einnehmen. Dargestellt wird dies in einer „Bloch-Kugel“. Die Richtung des Pfeils beinhaltet die jeweilige Quanteninformation zwischen 0 und 1. Diese Information ist bis zur Messung unbekannt. Die Messung zerstört die Überlagerung und lässt den Pfeil in 0 oder 1 springen. Ob 0 oder 1, das hängt von der Wahrscheinlichkeit für dieses Ergebnis ab, das aus einer bestimmten Überlagerung heraus entstehen kann.
© R. Wengenmayr / CC BY-NC-SA 4.0

Ein Quantennetzwerk benötigt ruhende und fliegende Qubits. Die ruhenden Qubits sitzen in Sendern und Empfängern, etwa künftigen Quantencomputern. Die fliegenden Qubits übertragen die Quanteninformation zwischen ihnen. Dafür sind Photonen ideal, denn sie sind lichtschnell und lassen sich kaum stören. Im Prinzip können sie Quanteninformation Tausende von Kilometern weit durch Glasfasernetze übermitteln. Und sie können mit geeigneten ruhenden Qubits verschränkt werden. Ein Quantenbit wird dabei in einem Photon als „Polarisation“ gespeichert, die wir uns als kleinen Zeiger vorstellen können. Er hat zwei Endpositionen für 1 und 0, kann aber auch „verdreht“ sein. Das entspricht dann einer bestimmten Überlagerung von 1 und 0. Die Übermittlung der Quanteninformation erfordert, dass das fliegende Quantenbit erst mit dem ruhenden Quantenbit des Senders und danach des Empfängers verschränkt wird. Nur so kann sie in ihrer speziellen Überlagerung von 0 und 1 übermittelt werden. Wird die Übertragung gestört, dann entspricht das einer Messung, und der Zustand springt in eine 0 oder 1. Das nutzt eine Form der sicheren Übermittlung verschlüsselter Nachrichten aus, der „Quantenkryptographie“: Schaltet sich ein Lauscher in eine verschränkte Übertragung ein, verrät er sich in den Messergebnissen des Empfängers.

Allerdings ist das Verschränken eines ruhenden mit einem fliegenden Qubit und umgekehrt eine Herausforderung. Hier hilft eine Technik, die Rempe als Pionier zur Perfektion getrieben hat. Dazu wird ein Rubidiumatom zwischen zwei Spiegeln eingefangen, die zu den besten der Welt gehören (s. Titelbild). Nun lässt ein Laserlichtimpuls passender Energie ein Elektron im Atom in einen höheren Quantenzustand springen. Dieser entspricht einer 1, der ursprüngliche Zustand niederer Energie einer 0. Nach kurzer Zeit fällt das Elektron wieder in den Grundzustand 0. Die freiwerdende Energie nimmt ein Photon mit. Das Atom leuchtet also und „sieht“ sich selbst viele tausend Mal in dem Spiegelkabinett. Das zwingt es, das Photon genau entlang der Achse des Spiegelkabinetts auszusenden. Das Photon flitzt wie ein Pingpong-Ball mehrere zehntausend Mal zwischen den beiden Spiegeln hin und her. So kommt es immer wieder an dem Atom vorbei, und irgendwann klappt es mit der Verschränkung. Zuvor wurde in das Atom mit Laserimpulsen die gewünschte Quanteninformation in Form einer bestimmten Überlagerung der Zustände 0 und 1 hineingeschrieben. Dieses Qubit übernimmt das Photon jetzt in seine Polarisation. Einer der beiden Spiegel ist nun etwas lichtdurchlässig. So gelangt das Photon irgendwann durch ihn hindurch in eine Glasfaser, die direkt in Achsenrichtung des Spiegelkabinetts angeschlossen ist. Diese leitet es weiter zum Empfänger: ein zweites Spiegelkabinett mit einem gefangenen Rubidiumatom. Mit ihm verschränkt sich das ankommende Photon in einem umgekehrten Prozess (Abb. B).

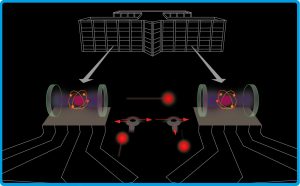
Abb. B: Verteiltes Rechnen. Zwei Atome als ruhende Quantenbits zwischen Spiegelpaaren, die sich in verschiedenen Laboren befinden, führen gemeinsam eine Quantenrechnung aus. Für die Verbindung sorgt eine Glasfaser. Durch diese sind mit den Atomen verschränkte Photonen als fliegende Qubits unterwegs, um die zu den Rechenschritten nötigen Quantenbits zwischen den Atomen auszutauschen.
© GCO nach einer Vorlage des MPI für Quantenoptik

Dank der Effizienz der Spiegelkabinette sind Gerhard Rempes Forschungsgruppen weltführend in der Entwicklung von Quantennetzwerken. Er interessiert sich aber nicht nur für technische Anwendungen, sondern fragt sich: „Wie groß kann man so ein verschränktes Quantenobjekt machen?“ Das ist eine grundlegende Frage der Physik, denn die Quantenmechanik gibt keine Grenze an. Den aktuellen Rekord hält ein chinesisches Team: Es sandte verschränkte Pho tonen über 1200 km weit bis zu einem Satelliten. Rempe hält aber Glasfasernetze für geeigneter, um das Quanteninternet oder ein lokales Quantennetzwerk aufzubauen. Auch dafür ist diese Frage entscheidend. Selbst ein künftiger Quantencomputer mit vielleicht Hunderten von Millionen Qubits muss sicherstellen können, dass sie überhaupt zu einem großen Quantenobjekt verschränkt werden können. Denn nur so kann er rechnen. Bei Quantencomputern sieht Rempe hier das Problem, dass sich viele, eng gedrängte Qubits gegenseitig stören. Auch deshalb forscht er an Quantennetzwerken. „Sie könnten viele kleine, gut voneinander isolierte Quantencomputer mit wenigen Qubits zu einem großen Quantencomputer verbinden“, sagt er. Aber wie funktionieren Quantencomputer? Und wozu sind sie gut?

Quantencomputer

Für solche Fragen ist Mari Carmen Bañuls Expertin. Sie forscht in der Theorie-Abteilung von Direktor Ignacio Cirac, einem Pionier des Quantenrechnens. Die Theoretikerin beschäftigt sich mit Algorithmen für Quantencomputer, also mit der mathematischen Basis der Programmierung. Aber worin wären Quantencomputer den herkömmlichen Computern überlegen? Mit einer primitiven Aufgabe wie „2 + 2“ tun sie sich erstaunlich schwer. Es gibt aber Aufgaben, in denen es herkömmlichen Computern so ergeht wie dem König in der Legende über die Erfindung des Schachspiels. Der ist so begeistert, dass der Erfinder sich eine Belohnung aussuchen soll. Im Gegensatz zum König kennt der Erfinder sich aber in Mathe aus und sagt: „Ich wünsche mir für das erste Feld des Schachbretts ein Reiskorn, das zweite zwei Körner und dann für jedes nächste Feld immer die doppelte Anzahl.“ Mathematisch ergibt das bei 64 Spielfeldern die gigantische von Zahl 1 + 2⁶³ Reiskörnern. Der König müsste umgerechnet rund 540 Milliarden Tonnen Reis herausrücken, das entspräche der Gesamtsumme von etwa neunhundert heutigen Weltjahresproduktionen. Das ist ein Beispiel für eine „exponentielle Explosion“, die alle herkömmlichen Computer überfordert. Deshalb können sie zum Beispiel Materialeigenschaften nicht exakt mit Hilfe der Quantenphysik berechnen, was die Entwicklung neuer Materialien behindert. In allen Materialien verbinden Elektronen als „Quantenkitt“ die Atome und bestimmen die chemischen und physikalischen Eigenschaften. Aber schon für einen winzigen Materialwürfel mit nur 100 solcher Elektronen müsste ein normaler Computer eine Matrix aus 2¹⁰⁰ x 2¹⁰⁰ Elementen berechnen können, erklärt Mari Carmen Bañuls. Nur so könnte er dessen Eigenschaften auf Basis der Quantenphysik präzise errechnen. Dabei käme eine Zahl heraus, die größer als die Anzahl aller Atome im Universum wäre. Ein Quantencomputer bräuchte für diese Aufgabe nur 100 Qubits – theoretisch. Ein anderes berühmtes Beispiel ist das „Problem des Handelsreisenden“. Der soll eine gewisse Anzahl von Städten besuchen und will dafür die kürzeste Strecke errechnen. Auch hier explodiert die Rechenzeit exponentiell mit der Anzahl der Städte. „Das entspricht einem Optimierungsproblem“, sagt Bañuls. Optimierungsprobleme gibt es überall, von Bahnverbindungen bis zum Design von Turbinen. Manche solcher Optimierungsaufgaben könnten Quantencomputer effizient lösen, andere nicht. Wo und warum das funktionieren könnte, daran wird heute intensiv geforscht.

Bañuls erklärt nun, wie Quantencomputer rechnen. Ein herkömmlicher Computer lädt beim Rechnen die Aufgabe, in Einsen und Nullen umgewandelt, zunächst in einen speziellen Speicher: das Register. „Dann wendet der Computer Logikoperationen wie UND, ODER, NICHT auf die im Register gespeicherte Information an“, erklärt sie. Solche Logikoperationen heißen „Gatter“ (Abb. C). Ein ODER-Gatter zum Beispiel hat zwei Eingänge und einen Ausgang. Liegt an beiden Eingängen jeweils eine 0 an, dann erzeugt ODER am Ausgang eine 0. Taucht an einem der Eingänge ein 1 auf, schaltet das Gatter im Ausgang auf 1 um. Technisch spielt sich das auf der unteren „Maschinenebene“ eines Computers ab, während auf der obersten Ebene ein Programm auf Basis von Algorithmen abläuft. „Ganz analog rechnet ein Quantencomputer“, erklärt Bañuls. Zuerst wird der Startwert der Quantenrechnung in ein Quantenregister aus Quantenbits geschrieben. Bei gespeicherten Atomen zum Beispiel geschieht das mit Laserimpulsen. Auf die so vorbereiteten Atome wird dann eine Abfolge von Quantengattern angewendet. Sie setzt den gewünschten Quantenalgorithmus um, also das auf höherer technischer Ebene ablaufende Programm.

Im Vergleich zu normalen Computern gibt es aber Unterschiede. Zum Beispiel fordert die Quantenmechanik, dass alle Prozesse zeitlich „reversibel“ sind. Wie ein Video müssen sie vorwärts wie rückwärts ablaufen können. Deshalb darf ein Quantengatter nur genauso viele Eingänge wie Ausgänge für die Quantenbits haben. Das ODER-Gatter scheidet damit aus, weil es mehrere Eingänge und nur einen Ausgang hat. Wenn es eine 1 errechnet, gibt es hinterher keine Information mehr darüber, an welchem der Eingänge eine 0 anlag. Eine solche Informationsvernichtung ist in der Quantenwelt verboten. Trotzdem lassen sich aber alle benötigten Operationen in Quantengatter umsetzen.

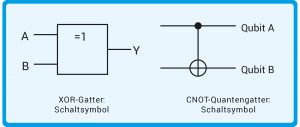
Abb. C: Logische Gatter und Quantengatter. Das „klassische“ Exklusiv-Oder-Gatter, kurz XOR-Gatter (englisch eXclusive OR“), besitzt zwei Eingänge A und B und einen Ausgang Y. Sobald an einem dieser Eingänge ein Bit 1 anliegt, erscheint am Ausgang eine 1. Das Gegenstück ist das Kontrolliertes-Nicht-Quantengatter CNOT (Controlled NOT). Es bildet diese logische Operation in einem Quantencomputer ab, umfasst aber auch noch die Überlagerungen von 1 und 0 während einer laufenden Quantenrechnung. So kann es beide Qubits miteinander verschränken. Im Unterschied zum XOR-Gatter muss das Quantengatter zwei Eingänge (links im Symbol) und zwei Ausgänge (rechts im Symbol) besitzen, damit seine Logikoperation umkehrbar (reversibel) bleibt.
© R. Wengenmayr / CC BY-NC-SA 4.0

Das eigentliche „Rechenwerk“ eines Quantencomputers ist die Verschränkung der beteiligten Qubits. Erst sie erzeugt die erforderliche Quantenparallelität. „Das ist der schwierige Teil“, erklärt die Physikerin. Für die Verschränkung der Qubits sorgen spezielle Operationen wie das CNOT-Gatter (Abb. C). Sobald alle Qubits so miteinander verschränkt sind, dass der gewünschte Quantenalgorithmus einprogrammiert ist, dürfen sie während der „Rechenzeit“ nicht gestört werden. Das ist ein bisschen wie beim Kochen in einem Schnellkochtopf: Den darf man erst öffnen, wenn das Gericht gar und der Druck abgebaut ist. Genauso muss man beim Quantencomputer lange genug warten. Dann macht man eine Messung und erhält ein Ergebnis, in Form von Einsen und Nullen. Das ist allerdings nicht das exakte Rechenergebnis! In der Quantenwelt passiert nämlich alles nur mit Wahrscheinlichkeiten, die allerdings präzise berechenbar sind. Also muss der Computer eine Quantenrechnung zum Beispiel tausend Mal wiederholen. Müsste er 2 + 2 ausrechnen, dann würde man als Ergebnisse eine Zahlenfolge von beispielsweise 3, 5, 1, 4… erhalten. Nach tausend Wiederholungen würde sich zeigen, dass am häufigsten die 4 herauskam: das korrekte Ergebnis.

Die größte Herausforderung auf dem Weg zu einem leistungsfähigen Quantencomputer ist die perfekte Isolierung der Qubits von der Umwelt. Heutige Geräte haben nur wenige Qubits, und schon nach wenigen Gatter-Operationen fällt die Rechnung den Störungen zum Opfer. Auf die nächste Forschungsgeneration warten noch viele spannende Herausforderungen, um leistungsfähige Quantencomputer und Quantennetzwerke zu entwickeln.

Abbildungshinweise:
Titelbild  © MPI für Quantenoptik
Abb. A: © R. Wengenmayr / CC BY-NC-SA 4.0
Abb. B: © GCO nach einer Vorlage des MPI für Quantenoptik
Abb. C: © R. Wengenmayr / CC BY-NC-SA 4.0

Der Text wird unter CC BY-NC-SA 4.0 veröffentlicht.

TECHMAX Ausgabe 36, September 2024; Text: Roland Wengenmayr; Redaktion: Dr. Tanja Fendt