Physik | Fächer | max-wissen.de

Das Diagramm zeigt die prozentuale Abschwächung des Sternlichts durch die Planetenatmosphäre in verschiedenen Wellenlängen, wenn der Planet WASP-39b vor dem Stern vorbeizieht (schwarze Punkte: Messwerte; dazugehörige Linien: Messunsicherheiten). Computerberechnungen (s. farbige Flächen) ergeben, dass vor allem Wasser, Kohlenstoffdioxid und Kohlenstoffmonoxid vorkommen.

Läuft der Planet vor seinem Mutterstern vorüber, spiegelt sich das im regelmäßigen Abfall und Anstieg der Helligkeitskurve.

Der Planet „zerrt“ an seinem Mutterstern. Dadurch bewegt sich dieser um den gemeinsamen Schwerpunkt des Systems. Sein Licht erscheint abwechselnd blau- und rotverschoben. Die Radialgeschwindigkeitsmethode misst diesen Dopplereffekt.

Im Tokamak-Experiment ASDEX Upgrade des Max-Planck-Instituts für Plasmaphysik in Garching wird an Kernfusion geforscht. Der Film zeigt einen Messtag beim Fusionsexperiment – vom Kontrollraum bis zu den Lasern und Lichtwellenleitern, die durch das Plasmagefäß geleitet werden. Die Dokumentation begleitet zwei Forschende während eines Arbeitstags und gibt Antworten auf die Frage, warum die Kernfusion als saubere Energiequelle großes Potenzial hat. Wissenschaftlerinnen und Wissenschaftler erklären, wie die Experimente in Garching den Weg für Großprojekte wie ITER oder andere Fusionskonzepte wie den Stellarator bereiten.

Die Printausgabe ist ab Anfang Dezember verfügbar. Vorbestellungen über den Warenkorb sind möglich.

Künstlerische Darstellung des Planetensystems TRAPPIST-1

In der Atmosphäre einer tiefblauen Welt regnet es gefährliche Glassplitter, eine andere hat die Konsistenz von Zuckerwatte, eine dritte besteht zum großen Teil aus Diamant. Alle diese seltsamen Orte mit so komplizierten Namen wie HD 189733b, WASP-193b und 55 Cancri e sind nicht irgendwelchen Science-Fiction-Filmen entsprungen, sondern sie existieren in den Weiten des Weltalls tatsächlich: Es handelt sich um Exoplaneten, die fremde Sterne umlaufen. Wie aber können Forschende solche Himmelskörper untersuchen? Wie lassen sie sich überhaupt aufspüren? Gibt es womöglich eine zweite Erde? Und was hat das James-Webb-Teleskop damit zu tun?

Anfang Oktober 1995 brach in Florenz eine neue Ära der Astronomie an. Michel Mayor und Didier Queloz von der Universität Genf hielten auf einem Kongress in der toskanischen Stadt einen bemerkenswerten Vortrag. Darin präsentierten sie nichts weniger als die Entdeckung eines Planeten außerhalb unseres Sonnensystems. Ihre Ergebnisse hatten sie ein Jahr zuvor am Observatorium Haute-Provence in Frankreich gewonnen. Im Fokus des dortigen Teleskops mit 1,93 Metern Spiegeldurchmesser stand ein unscheinbares, mit bloßem Auge gerade noch sichtbares Lichtpünktchen in der Konstellation Pegasus: der 50 Lichtjahre von der Erde entfernte, sonnenähnliche Stern 51 Pegasi. Für die Messungen nutzten die beiden Forscher einen am Teleskop montierten Spektrografen, der das Licht kosmischer Objekte in die Spektralfarben aufspaltet.

Im Spektrum eines Sterns finden sich viele dunkle Linien. Sie entstehen, wenn die Strahlung aus tiefer gelegenen, heißen Gasschichten durch kühlere geht. Dann schlucken die Elemente im Gas der kühleren Schichten das Licht bei bestimmten Wellenlängen und prägen dem Spektrum ihre Absorptionslinien auf. Anhand derer lässt sich die chemische Zusammensetzung eines Sterns bestimmen, denn jedes Element erzeugt einen charakteristischen Strichcode. Zudem können die Forschenden aus einem Spektrum auch Parameter wie Temperatur, Dichte oder die Dynamik des Gases herauslesen. Mayor und Queloz interessierten sich jedoch für die Bewegungen von Sternen, die Radialgeschwindigkeiten. Mayors Doktorand Didier Queloz hatte ein Computerprogramm geschrieben, das die gewonnenen Daten innerhalb kürzester Zeit verarbeitete. Aber welche Daten waren das?

Wenn Sterne tanzen

Wird ein Stern von einem Planeten umlaufen, wandern streng genommen beide Himmelskörper um den gemeinsamen Schwerpunkt. Dabei „zerrt“ der Planet aufgrund der gemeinsamen gravitativen Wechselwirkung rhythmisch am Stern. Blickt man seitlich auf das System, macht sich dessen Wackeln als Geschwindigkeitskomponente auf die Erde zu oder von ihr weg bemerkbar. Diese Radialgeschwindigkeit lässt sich anhand des Dopplereffekts messen. Den kennt jeder aus dem Alltag: Stehen wir auf einem Autobahnparkplatz, dann ändert sich die Tonhöhe eines schnell vorbeifahrenden Autos. Kommt das Fahrzeug auf uns zu, nehmen wir die Schallwellen als gestaucht wahr, unsere Ohren registrieren einen höheren Ton. Ist das Auto vorbeigeschossen, erscheinen uns die Schallwellen als gedehnt, der Ton klingt tiefer. Analog dazu zeigt das Licht eines Sterns, der sich uns nähert, wegen der kürzeren Wellenlänge eine Blauverschiebung; entfernt er sich von uns, erscheint das Licht aufgrund der längeren Wellenlänge rotverschoben (Abb. A). Was sich in der Theorie einfach anhört, ist in der Praxis umso schwerer. Denn die „Tanzschritte“ eines Sterns, die ein Planet hervorruft, sind im astronomischen Maßstab klein und laufen recht langsam ab. Doch die beiden Schweizer Wissenschaftler hatten die Präzision ihres Spektrografen derart ausgereizt, dass sie bei dem Stern 51 Pegasi eine Radialgeschwindigkeit von lediglich wenigen Dutzend Metern pro Sekunde registrieren konnten. Trotzdem bewegten sich die Daten an der Grenze des Messbaren. Dies führte dazu, dass manche Tagungsteilnehmer in Florenz mit Skepsis reagierten. Doch bereits eine Woche später bestätigte ein US-amerikanisches Forschungsteam, das in Konkurrenz zu Mayor und Queloz stand, deren Ergebnisse: Der erste „echte“ Exoplanet war gefunden!

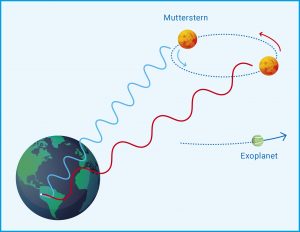
Schematische Darstellung der Radialgeschwindigkeitsmethode: Erde, Mutterstern, blaue und rote Lichtwellen; Exoplanet

Abb. A: Radialgeschwindigkeitsmethode. Der Planet „zerrt“ an seinem Mutterstern. Dadurch bewegt sich dieser um den gemeinsamen Schwerpunkt des Systems. Sein Licht erscheint abwechselnd blau- und rotverschoben. Die Radialgeschwindigkeitsmethode misst diesen Dopplereffekt.
© Verändert nach European Southern Observatory // CC BY 4.0

Tatsächlich hatten der polnische Astronom Aleksander Wolszczan und sein kanadischer Kollege Dale Frail bereits im Jahr 1992 die ersten beiden Planeten außerhalb des Sonnensystems aufgespürt. Doch diese Himmelskörper umkreisen nicht eine ferne Sonne, sondern den Pulsar PSR B1257+12 im Sternbild Jungfrau. Pulsare sind die Kerne von explodierten, sehr massereichen Sternen. Diese Neutronensterne besitzen Durchmesser von nur rund 20 Kilometern und bestehen, wie ihr Name verrät, vor allem aus Neutronen. Ein solcher stellarer „Zombie“ rotiert rasend schnell – PSR B1257+12 dreht sich 161-mal pro Sekunde um seine Achse – und sendet dabei über seine Pole gebündelte Strahlenkegel ins All, ähnlich einem Leuchtturm am Meer. Überstreichen sie die Erde, empfangen wir kurze, zeitlich begrenzte Pulse, daher die Bezeichnung Pulsar.

Ein Heißer Jupiter geht ins Netz

Der Stern 51 Pegasi trägt mittlerweile den Namen Helvetios. Sein Planet heißt Dimidium, was im Lateinischen so viel wie „Hälfte“ bedeutet, weil er knapp eine halbe Jupitermasse (0,46) aufweist. Er umläuft seinen Mutterstern in rund 4,2 Tagen im Abstand von ungefähr sieben Millionen Kilometern und ist ein Gasplanet mit einer Oberflächentemperatur von um die 1000 Grad Celsius. Dimidium war der erste Exoplanet vom Typ „Heißer Jupiter“, der gefunden wurde. Für ihre bahnbrechende Entdeckung erhielten Michel Mayor und Didier Queloz im Jahr 2019 den Nobelpreis für Physik. Zugleich eröffneten die beiden ein neues Forschungsfeld, das zu den spannendsten der modernen Astronomie gehört.

Bis zum Sommer 2025 waren laut dem NASA Exoplanet Archive rund 6000 Planeten bei fremden Sternen bekannt. Etwa 1000 befinden sich in Systemen mit mehreren Planeten. So etwa kreisen um den rund 40 Lichtjahre entfernten Stern Trappist-1 gleich sieben erdgroße Himmelskörper (s. Titelbild) . Viele Exoplaneten wurden mit der beschriebenen Methode der Radialgeschwindigkeitsmessung gefunden, einige auch mit anderen Verfahren wie dem sogenannten Mikrolinseneffekt. Dieser beruht darauf, dass nach der Allgemeinen Relativitätstheorie von Albert Einstein große Massen die Raumzeit verzerren und das Licht ablenken. Das wurde erstmals bei der totalen Sonnenfinsternis am 29. Mai 1919 beobachtet. Der Effekt tritt auch auf, wenn ein Stern mit einem Exoplaneten zwischen der Erde und einem fernen Hintergrundstern steht. Dann wird das Licht des Hintergrundsterns aufgrund der Gravitation des Planetensystems wie durch eine Linse gebündelt, und der Hintergrundstern erscheint für eine gewisse Zeit heller. Dadurch zeigt sich in der aufgezeichneten Lichtkurve eine zweite kleinere Spitze für den Exoplaneten. Allerdings muss dabei die Geometrie stimmen, das heißt, Beobachter, Planetensystem und Hintergrundstern müssen mehr oder weniger auf einer Linie stehen. Das ist selten der Fall, bisher wurden 260 Exoplaneten damit aufgespürt.

Einen ungleich größeren Teil fanden die Forschenden mit der Transitmethode (Abb. B) . Dabei wird direkt gemessen, wie sich die Helligkeit eines Sterns ändert, wenn ein dunklerer Begleiter vor ihm vorüberzieht. Das funktioniert nur, wenn der irdische Beobachter von der Seite auf die Umlaufbahn blickt. Im Grunde passiert dasselbe wie bei einer Sonnenfinsternis, wenn der Neumond über die Scheibe der Sonne wandert. Dabei ist die Lichtschwächung allerdings beträchtlich, weil Sonne und Mond von uns aus gesehen ähnlich groß am Himmel erscheinen und der Mond die Sonne im Idealfall vollständig abdeckt. Doch viele Lichtjahre von der Erde entfernte Exoplaneten sind winzig im Vergleich zu ihrem Mutterstern und reduzieren bei ihrem Durchgang dessen Licht nur wenig, erdgroße Planeten etwa im Promillebereich. Daher stoßen selbst Fotometer, welche die Intensität und den Helligkeitsverlauf von Sternenlicht messen, bei der Suche nach Exoplaneten an ihre Leistungsgrenze. Trotzdem waren und sind entsprechend ausgerüstete Satellitenobservatorien sehr erfolgreich. Allein das Weltraumteleskop Kepler hat während seiner Betriebszeit von 2009 bis 2018 rund 190.000 Sterne mit der Transitmethode untersucht und dabei mehr als 2500 bestätigte Planeten sowie Tausende Planetenkandidaten aufgespürt. Aktuell sucht sein Nachfolger TESS (Transiting Exoplanet Survey Satellite) ebenfalls mit der Transitmethode nach fernen Welten.

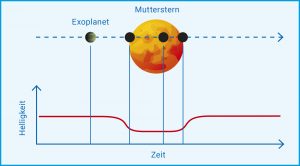
Schematische Darstellung der Transitmethode. Ein Exoplanet durchquert seinen Mutterstern, was zu Helligkeitsschwankungen führt, die in einem Diagramm über die Zeit angezeigt werden.

Abb. B: Transitmethode. Läuft der Planet vor seinem Mutterstern vorüber, spiegelt sich das im regelmäßigen Abfall und Anstieg der Helligkeitskurve.
© Verändert nach NASA Ames // Public Domain

Die Vermessung des Unbekannten

Ende des Jahres 2026 soll PLATO (PLAnetary Transits and Oscillation of stars) starten. Der europäische Satellit trägt 26 Kameras und wird in ausgewählten Himmelsfeldern die Helligkeitsabfälle von Sternen aufzeichnen, die Exoplaneten beim Transit verursachen. Zusammen mit Folgebeobachtungen von Teleskopen auf der Erde können dabei grundlegende Eigenschaften der Sterne und ihrer Planeten wie Radius, Masse und Alter exakt bestimmt werden. „Genaue Sternparameter sind unerlässlich für die korrekte Interpretation von Planetentransits, die Charakterisierung von Exoplaneten und das Verständnis der Architektur von Planetensystemen. So können wir bestimmen, welche Planeten bewohnbare, also lebensfreundliche Welten sind“, sagt Laurent Gizon, Direktor am Göttinger Max-Planck-Institut für Sonnensystemforschung. Sein Institut wird das Datenzentrum der Mission betreiben.

Längst sind die Zeiten vorbei, da man einfach nur neue Planeten entdecken wollte. Heute möchten Forschende die fernen Welten auch klassifizieren – wie Luis Thomas, Wissenschaftler in der Gruppe von Ralf Bender am Garchinger Max-Planck-Institut für extraterrestrische Physik. Obwohl die Bestimmung der Radialgeschwindigkeit schon länger als drei Jahrzehnte eingesetzt wird, leistet sie noch immer wertvolle Beiträge. Auch Thomas arbeitet damit. Er nutzt einen Spektrografen am Zwei-Meter-Teleskop der Universitätssternwarte München auf dem Gipfel des Wendelsteins in den bayerischen Alpen. „Mit dem Transitverfahren lassen sich zwar sehr viele Sterne gleichzeitig beobachten, aber es liefert nur den Radius eines Exoplaneten“, sagt der Forscher. Die Radialgeschwindigkeit hingegen erlaubt es, die Masse zu bestimmen. Beide Methoden ergänzen sich. „Und aus Masse und Radius können wir auf die Dichte des Planeten schließen“, so Luis Thomas. Die Parameter Dichte, Größe und Masse dienen der Beschreibung eines Exoplaneten. Tatsächlich unterscheiden die Forschenden mehrere Typen (s. Kasten). Hervorheben möchte Thomas die Subneptune: „Solche Objekte kennen wir in unserem Sonnensystem nicht, daher sind sie besonders interessant“, sagt er.

Die allermeisten der bisher bekannten Exoplaneten haben die Forschenden mit trickreichen Methoden indirekt nachgewiesen. Direkt beobachtet haben sie bisher lediglich wenige Dutzend. Das liegt daran, dass die Planeten nicht selbst leuchten und von ihren Muttersonnen überstrahlt werden wie ein Staubkörnchen von einer hellen Glühlampe. Das Weltraumteleskop James-Webb hat im Jahr 2024 seinen ersten Exoplaneten abgebildet – einen „Super-Jupiter“ bei dem zwölf Lichtjahre entfernten Stern Epsilon Indi. Gelungen war diese Entdeckung einem Team um Elisabeth Matthews vom Max-Planck-Institut für Astronomie in Heidelberg. Die Forschenden hatten das Bild mit einer Kamera aufgenommen, die den Stern mithilfe einer lichtundurchlässigen Maske bedeckte, auf diese Weise dessen Licht abschattete und somit gleichsam eine künstliche „Sternenfinsternis“ erzeugte. Derartige Aufnahmen haben noch Seltenheitswert.

Nicht so sehr um die bildliche Darstellung, sondern vielmehr um minutiöse Messungen geht es Astronominnen und Astronomen in der Gruppe von Laura Kreidberg am Heidelberger Institut. Sie nutzen dazu ebenfalls das James-Webb-Teleskop, das seit dem Jahr 2022 mit seinem Sechs-Meter-Spiegel das All durchmustert. Damit gewinnen sie Transmissionsspektren (Abb. C) der Atmosphären von Exoplaneten, wie etwa von heißen Gasriesen. Diese Methode funktioniert folgendermaßen: Zieht ein Planet vor seinem Mutterstern vorbei, fällt dessen Licht durch die mehr oder weniger dünne Atmosphäre des Planeten. Die darin enthaltenen Elemente und Verbindungen hinterlassen im Sternspektrum ihre Fingerabdrücke. Die Kunst besteht nun darin, diese in den Daten aufzuspüren und den Stoffen zuzuordnen.

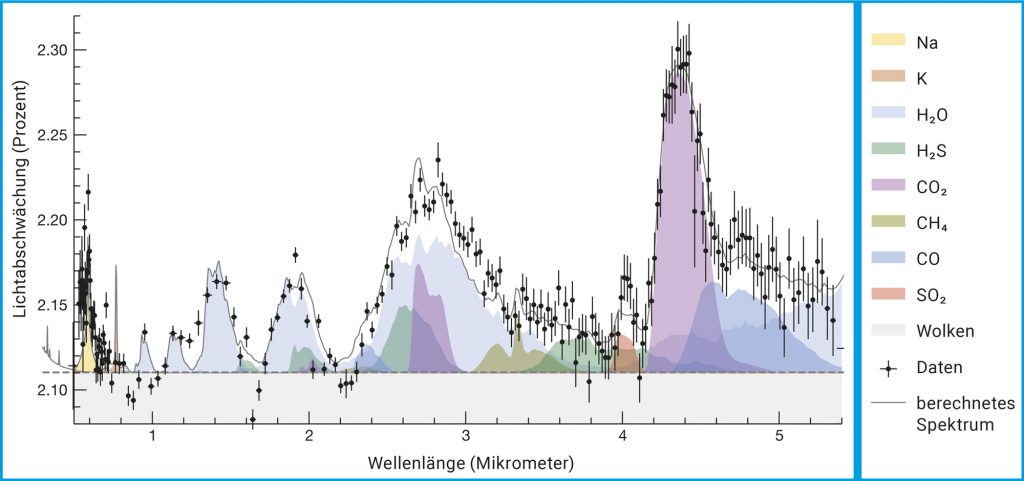
Diagramm, das die prozentuale Abschwächung des Sternenlichts durch die Planetenatmosphäre in verschiedenen Wellenlängen zeigt. Die Messungen beziehen sich auf den Planeten WASP-39b.

Abb. C: Transmissionsspektrum des heißen Jupiter WASP-39b. Das Diagramm zeigt die prozentuale Abschwächung des Sternlichts durch die Planetenatmosphäre in verschiedenen Wellenlängen, wenn der Planet WASP-39b vor dem Stern vorbeizieht (schwarze Punkte: Messwerte; dazugehörige Linien: Messunsicherheiten). Computerberechnungen (s. farbige Flächen) ergeben, dass vor allem Wasser, Kohlenstoffdioxid und Kohlenstoffmonoxid vorkommen.
© Z. Rustamkulov et al., Nature Vol. 614, 659 (2023) // CC BY 4.0

Lebensspuren im Weltall

Hier setzen die Forschungen der Abteilung APEx (Atmosphärenphysik der Exoplaneten) von Laura Kreidberg an. „Die Zusammensetzung der Atmosphäre und das Klima auf einem fernen Planeten zu erforschen, stellt höchste Ansprüche an die Beobachtungstechnik, was mich sehr fasziniert“, sagt sie. Das James-Webb-Teleskop beobachtet im langwelligen, infraroten Spektralbereich und kann so zu kühleren, vielleicht sogar bewohnten Welten vordringen. Denn die Absorptionslinien in den Infrarotspektren stammen nicht nur von Atomen, sondern auch von Molekülen. Und diese können auf organischen Ursprung hinweisen. Einer der Arbeitsschwerpunkte der Wissenschaftlerin ist das Studium von Supererden und erdähnlichen Exoplaneten. Wie entsteht die Vielfalt der Planetensysteme? Wie sehen die Planeten heute aus? Wie haben sie sich im Laufe der Zeit verändert? Gibt es eine belebte Erde 2.0?

Die Suche nach Lebensspuren auf fremden Welten gehört zu den aufregendsten Kapiteln der Forschung. Dazu müssen die Exoplaneten eine Reihe von Bedingungen erfüllen. So darf es auf ihnen nicht zu heiß und nicht zu kalt sein. Im Idealfall stellen sich auf der Oberfläche Temperaturen ein, bei denen Wasser – eine wichtige Essenz für Leben, wie wir es kennen – flüssig ist. Kreist ein Planet in der habitablen Zone, ist diese Bedingung per Definition erfüllt. Zudem sollte der Exoplanet eine Atmosphäre besitzen, die das Klima stabilisiert und eventuelles Leben vor der starken Strahlung der Muttersonne schützt. Sterne wie die Sonne strahlen recht „ruhig“, von gelegentlichen Massenauswürfen und Flares einmal abgesehen. Anders verhält es sich bei der Klasse der Roten Zwerge: Diese machen etwa drei Viertel aller Sterne in unserer Milchstraße aus, sind kleiner und kühler als die Sonne und meist recht „unruhig“. Um auf lebensfreundliche Temperatur zu kommen, müssen Planeten in geringem Abstand um sie kreisen. Dadurch spüren sie die große Aktivität Roter Zwerge besonders stark – was Leben auf den Planeten schaden kann.

Mit dem James-Webb-Teleskop haben Laura Kreidberg und ihr Team zehn Gesteinsplaneten um Rote Zwerge untersucht und bei keinem eine Atmosphäre gefunden. „Mehrere Transmissionsspektren zeigen vorläufige Hinweise auf molekulare Absorptionsmerk-male, aber diese Hinweise sind nur geringfügig signifikant, und die Spektren könnten durch stellare Verunreinigungen beeinflusst sein“, schreiben Kreidberg und ihr Kollege Kevin B. Stevenson von der US-amerikanischen Johns Hopkins University in einem Fachartikel im Sommer 2025.

Wenn sich um jene Planeten überhaupt Atmosphären mit Sauerstoff, Stickstoff oder Kohlenstoffdioxid befinden, sind diese Moleküle so spärlich vertreten, dass sie sich mit heutigen Messmethoden nicht nachweisen lassen. Vielleicht aber hat sich eine Atmosphäre bei der Planetengeburt erst gar nicht gebildet? Oder sie wurde durch die starke UV- und Röntgenstrahlung des Roten Zwergs weggeblasen? Künftige Beobachtungen von Exoplaneten um sonnenähnliche Sterne könnten helfen, das Geheimnis zu lüften. Die Suche nach der zweiten Erde geht weiter!

Abbildungshinweise:
Titelbild: © ESO/M. Kornmesser
Abb. A: © Verändert nach European Southern Observatory // CC BY 4.0
Abb. B: © Verändert nach NASA Ames // Public Domain
Abb. C: © Z. Rustamkulov et al., Nature Vol. 614, 659 (2023) // CC BY 4.0

TECHMAX Ausgabe 40, November 2025; Text: Helmut Hornung; Redaktion: Tanja Fendt

Mithilfe von KI eine Filmsynchronisation nachbessern oder Science-Fiction-Figuren zum Leben erwecken? Mit seinem Team forscht der Informatiker Christian Theobalt an der Schnittstelle von Computer-Vision, Computer-Grafik und künstlicher Intelligenz.

Zum Podcast (36 min) vom 3. September 2025 © detektor.fm / Max-Planck-Gesellschaft

08:40 | Forschungsprojekte für die Filmbranche: Motion-Capture-Verfahren optimieren

13:20 | Anwendungsbeispiele in der Medizin (Untersuchung des Bewegungsapparates)

19:06 | Kann man die Mimik in Echtzeit von einer Person auf eine andere übertragen?

Bild: © [M] MPG; Roboter im Atelier: [AI] Midjourney / MPG; Vitruvianischer Mensch: Leonardo da Vinci , Foto: Luc Viatour / ucnix.

Das Titelbild des Heftes zeigt zwei stilisierte virtuelle Köpfe. Sie stellen eine KI dar.

Forschende machen sich neugierig und motiviert auf die Suche nach neuem Wissen. Und mit einer guten Portion Kreativität und Ausdauer können sie Neues entdecken und verstehen. Künstliche Intelligenz ist zunehmend ein wichtiges Hilfsmittel, um dieses Ziel zu erreichen. Doch könnte die KI auch selbst als Wissenschaftlerin agieren, zu Erkenntnissen gelangen oder Ideen, Konzepte und echtes Verständnis entwickeln?

Noch nicht einmal fünf Jahre alt und schon das Abitur gut bestanden: Deutsch 2, Geschichte 2, Mathe 2, Ethik 2, Informatik 2. Die Hochbegabte: die künstliche Intelligenz (KI) ChatGPT, die auf einem großen Sprachmodell (large language model, LLM) basiert. Und wie sich anhand von Aufgaben aus dem bayerischen Abitur zeigte, war die 2023 verfügbare Version GPT-4 bereits so weit entwickelt, dass sie als gute Schülerin durchging und die allgemeine Hochschulreife zugesprochen bekam. Doch bedeutet das, dass die KI tatsächlich intelligent ist, oder plappert sie nur wie ein gut trainierter Papagei die richtigen Phrasen im richtigen Moment? Dass sie bekanntes Wissen korrekt und verständlich wiedergeben kann, hat KI schon gezeigt. Aber kann sie auch für die menschliche Intelligenz entscheidende Eigenschaften wie Neugier, Motivation und Kreativität entwickeln, Aufgaben eigenständig bearbeiten und sich eine eigene Meinung bilden? Mit diesen Fragen beschäftigt sich der Physiker Mario Krenn. Am Max-Planck-Institut für die Physik des Lichts und an der Eberhard Karls Universität Tübingen arbeitet er an einer KI, die Wissenschaftlerinnen und Wissenschaftler unterstützt oder sogar eigenständig forscht.

Neue Lösungen für Experimente

Zu dieser Forschung gelangte Krenn über die Quantenoptik. Im Jahr 2014 arbeitete er als Doktorand im Labor des späteren Nobelpreisträgers Anton Zeilinger in Wien daran, in komplexen optischen Aufbauten Lichtteilchen mit besonderen Eigenschaften herzustellen. Doch an einer Aufgabe biss Krenn sich monatelang die Zähne aus. Zusammen mit weiteren Forschenden versuchte er sich einen experimentellen Aufbau zu überlegen, der Lichtteilchen herstellt, die eine ganz bestimmte Beziehung zueinander haben. Egal wie er Laser, Linsen, Spiegel, Kristalle und Detektoren in seinen Gedankenexperimenten, Skizzen und Berechnungen anordnete, das erwünschte Ergebnis blieb aus. Also entschied Krenn sich dazu, ein Computerprogramm zu entwickeln, das sich auf die Suche nach der Lösung für sein Problem machen sollte. Dazu stattete er das Programm mit physikalischem Grundwissen aus und stellte alle optischen Bauteile virtuell zur Verfügung. „Damals wie heute setzen wir dazu sogenannte Explorationsalgorithmen ein, die den riesigen abstrakten Raum an Kombinationen sehr effizient auf neue Lösungen durchsuchen“, sagt Krenn. Melvin, wie Krenn sein Programm taufte, simulierte also Millionen von Kombinationen der Bauelemente und hatte damit schnell Erfolg. „Das war ein verrückter Tag. Ich konnte das gar nicht glauben. Das Programm hatte in ein paar Stunden eine Lösung gefunden, nach der drei experimentelle und ein theoretischer Physiker monatelang gesucht hatten“, erzählt Krenn. Anschließend sorgte er dafür, dass Melvin dazulernen konnte. Dank eines Algorithmus des maschinellen Lernens erinnert sich das Programm an bereits simulierte Aufbauten und versucht, diese für die Lösung des neuen Problems wiederzuverwerten.

Ausgehend von diesem Erfolg untersucht Krenn, wie KI der Forschung helfen und zu neuen Erkenntnissen beitragen kann. Schon heute ist KI ein wichtiges Hilfsmittel: So kann beispielsweise AlphaFold, das auf tiefen neuronalen Netzen basiert, eine Proteinstruktur auf Grundlage der Aminosäuresequenz vorhersagen. Dies ermöglicht es, genau auf eine Anwendung zugeschnittene Proteine herzustellen. Und deren Potenzial ist riesig, etwa in der Medizin oder chemischen Industrie. Doch neues Verständnis hat AlphaFold bisher nicht produziert. So sagt das Programm zwar voraus, wie die Struktur eines Proteins einer bestimmten Aminosäuresequenz aussieht, erklärt aber nicht, warum es diese Form annimmt oder wie die Faltung abläuft.

Maschinen forschen mit

Krenn wünscht sich aber eine KI, die mehr ist als eine Blackbox, die ein Ergebnis produziert. Daher untersucht er, wie KI auf unterschiedlichen Ebenen zu neuem Verständnis beitragen kann (Abb. A). In der ersten Dimension dient KI als Instrument, das Eigenschaften eines Systems aufdeckt, die sonst nur schwer oder gar nicht zu ergründen sind. Menschen können aus diesen Erkenntnissen dann wissenschaftliches Verständnis entwickeln. Dies gilt vor allem für die Simulation von natürlichen Prozessen, die auf Längen- und Zeitskalen ablaufen, die im Experiment nicht wahrnehmbar sind. In der zweiten Dimension dient die KI als Inspirationsquelle für neue Konzepte und Ideen, die menschliche Forschende verstehen und verallgemeinern können. So kann die KI Überraschungen in Datensätzen oder der Literatur finden. Oder unerwartete Konzepte entdecken, indem sie wissenschaftliche Modelle untersucht oder mit einprogrammierter Neugier oder Kreativität einen Datenraum exploriert. Und auch wenn die KI Lösungen für bestimmte Probleme beziehungsweise Aufgaben in interpretierbarer Form ausgibt, kann sie als Inspirationsquelle für die Entdeckung neuer Konzepte dienen. In diesen ersten beiden Dimensionen ermöglicht die KI also dem Menschen, neue wissenschaftliche Erkenntnisse zu gewinnen. In der dritten Dimension gewinnt die Maschine selbst neue Erkenntnisse und damit Verständnis und kann dieses auch weitergeben. In diese Dimension ist KI bisher nicht vorgedrungen.

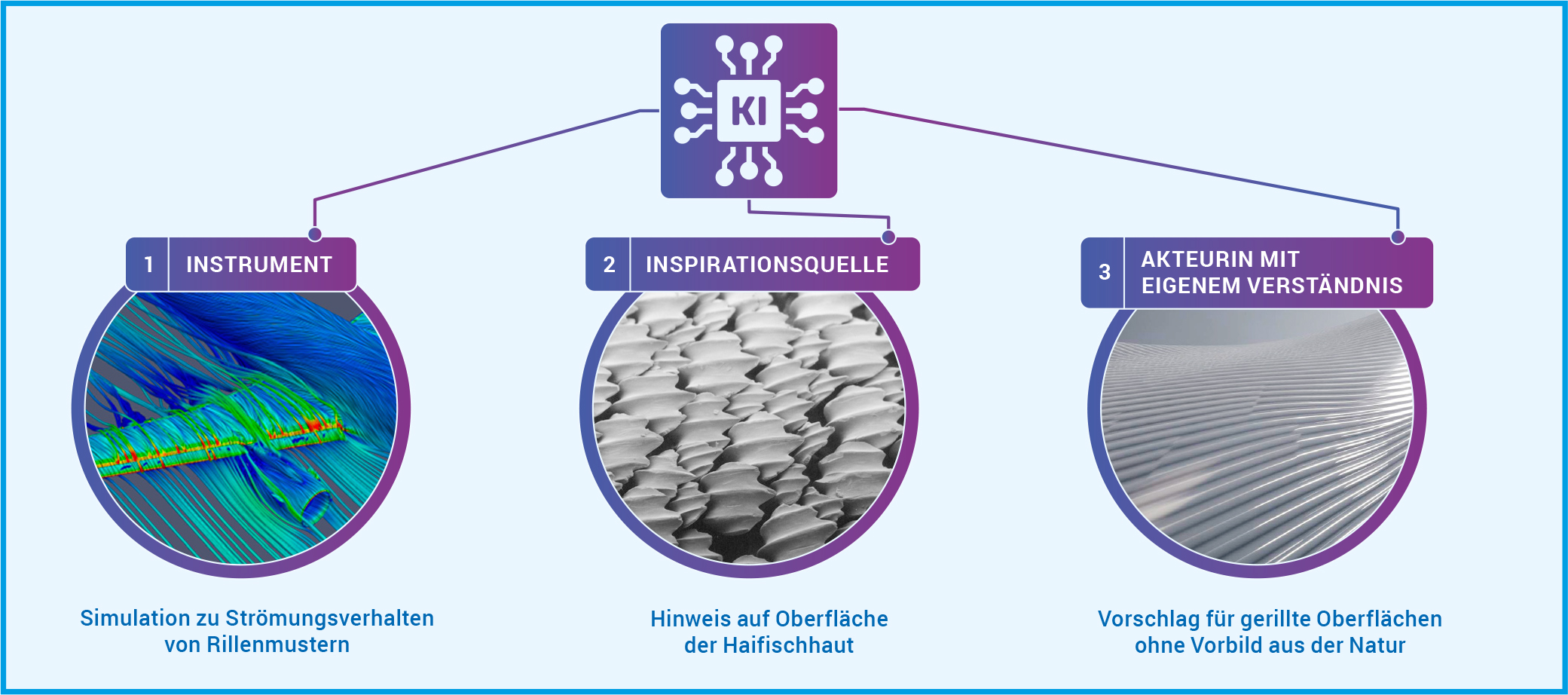
Die Abbildung verdeutlicht schematisch, wie KI auf drei Dimensionen zu neuem wissenschaftlichem Verständnis beitragen kann. Links: KI als Instrument, symbolisiert durch ein Bild mit einem Flugzeugflügel und Strömungsmustern. Mitte: KI als Inspirationsquelle, symbolisiert durch ein Bild mit Haifischhaut. Rechts: KI als Agentin mit eigenem Verständnis, symbolisiert durch ein Bild mit einer gerillten Oberfläche.

Abb. A: KI kann auf drei Dimensionen zu neuem Verständnis beitragen. [ 1 ] Als Instrument, das Eigenschaften eines physikalischen Systems aufdeckt, die sonst nur schwer oder gar nicht zu ergründen sind. Bei der Haifischhaut hätte eine KI durch Simulationen die Experimente in einem Strömungskanal ersetzen können. [ 2 ] Als Inspirationsquelle, die überraschende Ideen und Konzepte findet. Die KI hätte etwa Forschende aus der Luft- und Raumfahrt auf die Beobachtungen des Wirbeltierforschers aufmerksam machen können, der die Rillen auf den Haifischschuppen entdeckte. [ 3 ] Als Agentin des Verständnisses, die selbst in der Lage ist, wissenschaftliches Verständnis zu entwickeln und weiterzugeben. So eine Agentin hätte auch ohne das biologische Vorbild der Haifischhaut auf derartige Rillen kommen können, um den Strömungswiderstand von Flugzeugen zu reduzieren.
© DLR (CC BY-NC-ND 3.0), Pascal Deynat/Odontobase (CC BY-SA 3.0), MPG (CC BY-NC-SA 4.0)

Algorithmen erzeugen Forschungsfragen

Mario Krenn arbeitet aktuell an einer KI als Inspirationsquelle. Zusammen mit seiner Kollegin Xuemei Gu entwickelte er SciMuse, die Wissenschafts-Muse: Ein System, das neue, personalisierte Forschungsideen vorschlägt. Dazu stützten sich die Forschenden einerseits auf GPT-4 und setzten andererseits auf einen selbst entwickelten Wissensgraphen (Abb. B). Der Wissensgraph enthält Informationen zum Inhalt und Einfluss von mehr als 58 Millionen wissenschaftlichen Artikeln. Während der Entwicklung von SciMuse nutzten die Forschenden entweder eine Kombination aus ihrem Wissensgraphen und GPT-4 oder GPT-4 alleine, um Forschungsvorschläge zu generieren. Dabei beinhalteten die Prompts für GPT-4 die Aufforderung zur Selbstreflexion: GPT-4 sollte drei Ideen entwickeln, reflektieren und zweimal verbessern. Und dann die am besten geeignete Projektidee als Endergebnis auswählen. Eine derartige Selbstreflexion ist in zahlreichen aktuellen LLM-KIs bereits enthalten, so auch in der GPT-4 Nachfolgerin o3. Diese sogenannten Reasoning-Modelle überprüfen ihre eigenen Ergebnisse schrittweise, bevor sie eine Antwort geben.

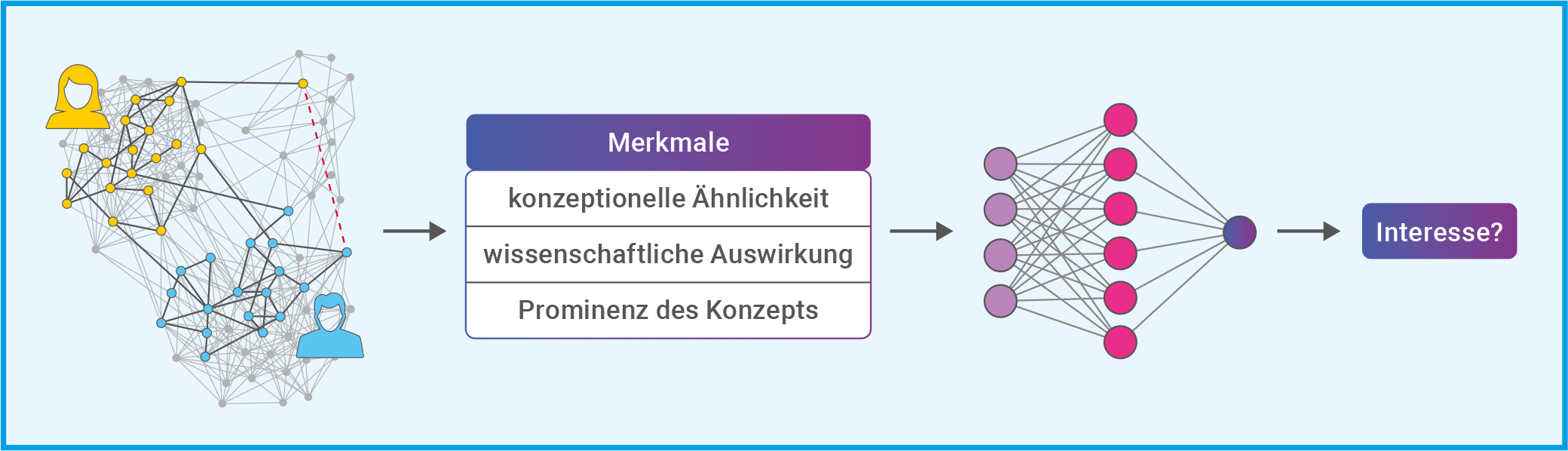
Die Abbildung zeigt links einen Wissensgraphen, der mit verschiedenfarbigen Linien, die sich kreuzen, symbolisiert wird. In der Mitte sind Merkmale aufgelistet, rechts ist ein neuronales Netz mit einer verborgenen Schicht und einem Ausgabeneuron durch Kreise mit Linien symbolisiert.

Abb. B: Im Wissensgraphen (links) repräsentieren die Kreise (Eckpunkte) wissenschaftliche Konzepte. Und jedes Mal, wenn zwei Konzepte gemeinsam in einem Titel oder der Zusammenfassung einer wissenschaftlichen Arbeit erscheinen, wird eine Verbindungslinie (Kante) gezogen. Der gelbe und der blaue Teilgraph repräsentieren die Arbeit zweier Forschender, für die ein gemeinsamer Forschungsvorschlag gesucht wird. Die Merkmale der Konzepte im Wissensgraphen (Mitte) beeinflussen das Interesse an den Forschungsvorschlägen erheblich. Auf Grundlage dieser Daten wurde ein maschinelles Lernmodell trainiert, um den Grad des Interesses allein auf der Grundlage dieser Eigenschaften vorherzusagen. Als Lernmodell wurde ein kleines neuronales Netz (rechts) mit einer verborgenen Schicht und einem Ausgabeneuron genutzt (s. Techmax 34, Abb. B).
© Verändert nach: Gu & Krenn (2024): Generation and human-expert evaluation of interesting research ideas using knowledge graphs and large language models; OpenReview.net / CC BY 4.0

Krenn und Gu legten im nächsten Schritt einhundert erfahrenen Max-Planck-Forschenden die KI-generierten, personalisierten Forschungsvorschläge vor. In einer Umfrage bewerteten diese das Interessensniveau der Vorschläge. Die Ergebnisse zeigten, dass die Forschungsvorschläge, die mittels einer Kombination von Wissensgraph plus GPT-4 erstellt wurden, nicht besser abschnitten als jene, die von GPT-4 alleine erzeugt wurden. Doch anhand der Bewertungen konnten die Forschenden klare Zusammenhänge zwischen Interessensniveau des Forschungsvorschlags und Eigenschaften nachweisen, die die zugrunde liegenden Konzepte im Wissensgraphen aufwiesen (Abb. B). Anhand dieser Zusammenhänge trainierte Krenns Team ein kleines neuronales Netz für die Vorhersage des Forschungsinteresses allein aus Daten des Wissensgraphen. Damit hatten sie die KI mit einem Gefühl für spannende Forschungsthemen ausgestattet und so SciMuse geschaffen. Dank dieses Gefühls kann SciMuse neue und hochinteressante Forschungsthemen aus Wissensgraphen auswählen und mit Hilfe moderner großer Sprachmodelle vollwertige Forschungsvorschläge formulieren.

Große Sprachmodelle

GPT-4 konnte Krenns Team nicht auf die gleiche Weise mit Gefühl ausstatten. Denn während sie im selbst entwickelten Wissensgraphen bestimmte Eigenschaften ausmachen konnten, die das Interessensniveau beeinflussen, haben sie keinen Einblick in die Arbeitsweise von GPT-4. LLMs wie GPT-4 sind meist eine Blackbox, die so komplex ist, dass niemand genau versteht, wie sie auf ihre Ergebnisse kommt. Ein LLM basiert auf einem künstlichen neuronalen Netz, das auf die Verarbeitung und Erzeugung von natürlicher Sprache spezialisiert ist. Ein oftmals genutzter Ansatz, um ein LLM zu erzeugen, ist der generative vortrainierte Transformer (generative pre-trained transformer, GPT). Dieser ist darauf spezialisiert, Text zu verarbeiten und zu erzeugen. Dabei wird Text in numerische Repräsentationen (Token) umgewandelt. Jedes Token wird gemäß einer Worteinbettungstabelle (word embedding) in einen Vektor umgewandelt und so in Kontext gesetzt (Abb. C). Das künstliche neuronale Netz trainiert bei GPTs auf riesigen Datensätzen unmarkierten Textes (unüberwachtes Lernen). Zur Feinabstimmung wird überwachtes Lernen und Verstärkungslernen durch menschliches Feedback eingesetzt.

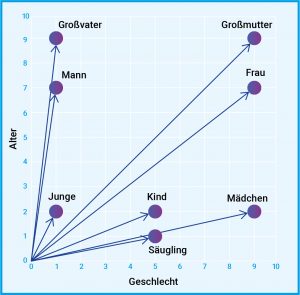
Die Abbildung zeigt zwei Dimensionen „Alter“ und „Geschlecht“ und darin einsortiert die Darstellung von Wörtern (wie zum Beispiel Junge, Mädchen, Säugling) als Vektorpfeile.

Abb. C: In der natürlichen Sprachverarbeitung ist eine Worteinbettung eine Darstellung eines Wortes. In der Regel handelt es sich bei der Darstellung um einen Vektor, der die Bedeutung des Wortes so kodiert, dass bei Wörtern, die im Vektorraum näher beieinander liegen, eine ähnliche Bedeutung zu erwarten ist. Der Vektor kann dabei vieldimensional sein, hier ist ein Beispiel in 2D dargestellt. Dabei werden Wörter gemäß ihrer Bedeutung in die Dimensionen Alter und Geschlecht eingeordnet.
© MPG

Aktuelle große Sprachmodelle wirken schon erstaunlich intelligent. Im Fall der Reasoning-Modelle sprechen einige Fachleute sogar davon, dass diese Modelle nun logisch denken können. Kritiker bezweifeln dies und sehen den Schritt hin zur allgemeinen künstlichen Intelligenz (artificial general intelligence, AGI) noch in weiter Ferne. Unter AGI versteht man eine KI, die eigene Schlüsse zieht, sowie Bekanntes und Gelerntes auf neue Felder übertragen kann. Außerdem sollte eine AGI in einer natürlichen, das heißt einer komplexen und offenen Umgebung zurechtkommen. Wenn es um die Bewertung der Intelligenz einer KI geht, wird es schnell philosophisch. Denn es ist nicht ganz klar, was intelligent genau bedeutet. Schon heute überflügeln KIs den Menschen in zahlreichen Kategorien des rationalen Denkens. Doch bisher scheitern KIs daran, auf unerwartete Veränderungen zu reagieren oder ihr Gelerntes auf Gebiete anzuwenden beziehungsweise zu übertragen, die nicht ihrem Training entsprechen. Eine KI, die selbst als Wissenschaftlerin agieren soll, müsste genau das schaffen, um neue Erkenntnisse zu gewinnen und Verständnis zu entwickeln. Denn Verständnis setzt eine intuitive, modell- oder bildhafte Vorstellung eines wissenschaftlichen Zusammenhangs voraus. Diese Vorstellung ermöglicht es dann, qualitative Aussagen zu treffen, ohne genaue Berechnungen anzustellen.

Für die KI als Wissenschaftlerin sind außerdem auch Neugier, Kreativität und Motivation wichtig. Dazu braucht sie eine Beziehung zur realen Welt. Denn um spannende, das heißt bedeutende Probleme beziehungsweise Fragen zu identifizieren, muss sie wissen, was ihr selbst oder für die ganze Menschheit wichtig ist. Dieses sogenannte Weltwissen ist bei KIs bisher wenig ausgeprägt. Das liegt an den eingeschränkten Trainingsdaten, die KIs bisher zum Lernen nutzen. Zwar könnte man bei großen Sprachmodellen wie ChatGPT davon sprechen, dass sie sich durch die enorme Anzahl an verarbeiteten Texten Weltwissen angeeignet haben. Doch auch ihnen fehlt der vieldimensionale Bezug zur Welt, weil sie im Gegensatz zum Menschen keine verkörperten Intelligenzen sind: Sie können nicht physisch mit der realen Welt interagieren und auch nur sehr eingeschränkt Sinneseindrücke sammeln. Während also ein Mensch sowohl Auto fahren als auch wissenschaftliche Erkenntnisse gewinnen kann, ist dies für KIs momentan noch eine Herausforderung.

Mario Krenn bewertet die Fähigkeiten von KI als Wissenschaftlerin aktuell so: „Wir sind jetzt auf dem Niveau, auf dem wir Ideen erzeugen können. Und bei bestimmten Themen können unsere KI-Systeme bereits vollkommen neue Lösungen für wissenschaftliche Fragestellungen finden!“ Für die Zukunft ist er optimistisch und hofft, dass die KI ihre menschlichen Kolleginnen und Kollegen auf der Suche nach neuen Erkenntnissen bald kräftig unterstützt.

TECHMAX Ausgabe 39, August 2025; Text: Dr. Andreas Merian; Redaktion: Dr. Tanja Fendt

Zwei Podcast-Folgen beleuchten verschiedene Aspekte zum Einsatz künstlicher Intelligenz in der Medizin.

KI und bildgebende Verfahren
Zum Podcast (28 min) vom 9. Juli 2025 © detektor.fm / Max-Planck-Gesellschaft
Themen: Deep Learning // Explainable Artificial Intelligence // Auswertung von MRT-Bildern mit KI

KI in der Biomedizin
Zum Podcast (35 min) vom 12. Juni 2025 © detektor.fm / Max-Planck-Gesellschaft
Themen: Ethische Fragen beim Einsatz von KI im Gesundheitswesen // Oszillierende Neuronale Netze // KI hilft bei der Berechnung von biologischen Abläufen

Die Verschränkung macht das E91-Übertragungsprotokoll noch sicherer. Nachteil: Ihre besondere Empfindlichkeit gegen Störungen erhöht den technischen Aufwand.